Verifying Sweden's Impressive Covid Performance

Resolving the best dataset to use for Sweden

NOTE: This is a very technical post! It’s a deep dive into the methodological differences of two different Covid datasets, to figure out which one is most accurate. If you just want the conclusion, scroll to the end.

In September, I wrote a post estimating the impact of Sweden’s no-lockdown policy. I concluded that Sweden did have more deaths than most of its neighbors, but that the difference was small; each Swedish citizen lost a couple extra days of life.

More recent data change that picture.

Claim: Sweden did better than its neighbors

This viral tweet says that data from the OECD (an intergovernmental association of developed countries) show that Sweden actually had the lowest excess death rate:

James Melville @JamesMelville

Sweden 🇸🇪 🇸🇪 No lockdowns 🇸🇪 No school closures 🇸🇪 No mask mandates Sweden had the lowest overall cumulative excess deaths in countries analysed by the OECD during the pandemic era from March 2020 to June 2022.

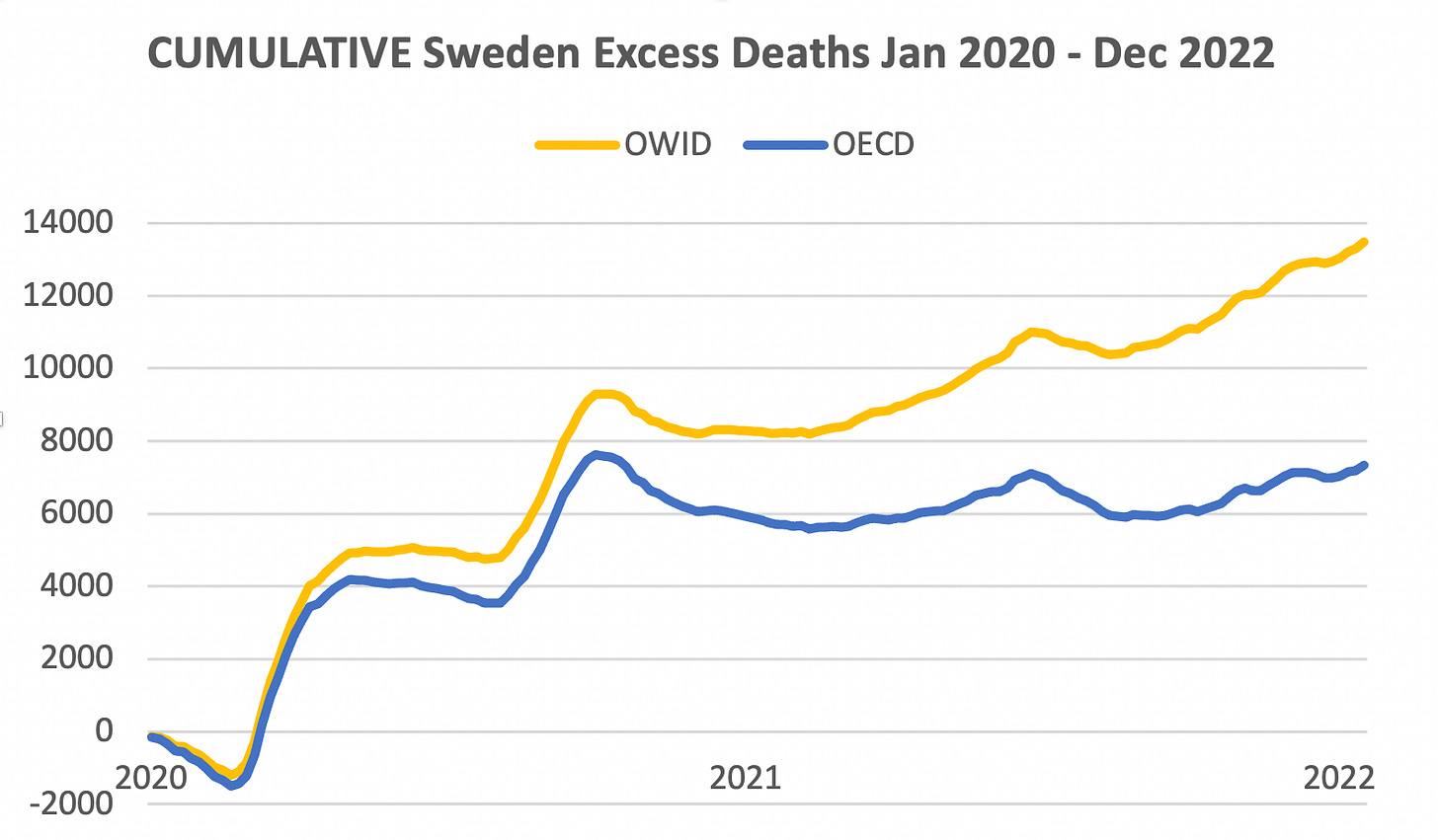
That contradicted my post, which used data from Our World in Data (OWID), which I had also cross-checked with the World Health Organization (WHO). Here was my graph, covering the same timeframe:

The OWID/WHO data show Sweden doing significantly worse than Norway and Denmark, while the OECD shows Sweden doing better.

But the two datasets can’t both be right!

Since I knew my data was from a reputable place, I was skeptical about that tweet above. It claimed to cite the OECD, a reliable intergovernmental organization – but did the OECD really even say that?

Thinking I’d quickly debunk the chart, I went to the OECD database and crunched their numbers. But they confirmed the chart. I also checked Eurostat, which also was in line with the OECD.

Here’s how much the OECD data differs from OWID, graphically:

Why would the OECD dataset show such different numbers from the OWID and WHO datasets?

(Note: WHO’s dataset hasn’t been updated for 2022, so I’ll focus on OWID from here on out.)

OECD fails to consider all Swedish deaths

After a lot of cross-checking, I noticed one straightforward issue with the OECD data. While they correctly and precisely copy weekly deaths as reported by the Swedish government, they fail to consider deaths which were not classified with any week.

As OWID notes in their methodology:

“Sweden has a significant number of deaths which occurred in an "unknown" date (and thus week) in all years. However, 95% these have a known month of death.”

So OWID reasonably assigns those deaths to weeks within the month that they happened. It’s not perfect (it can’t be, since the exact date isn’t known) but it seems much better than ignoring such deaths.

I applied that change to OECD’s dataset, and doing so causes their estimate to rise — eliminating about half of the gap between excess mortality predictions.

In the below graph, the dark blue OCED line would rise to the light-blue line:

But there is still a lot of daylight between the yellow OWID estimate and the light-blue fixed-OECD estimate.

That turns out to hinge on a methodology difference:

Different methods to estimate “baseline” deaths

I thought maybe the OECD had some odd methodology, but it turned out that they use the most straightforward method: They take the average number of deaths for each week in the pre-pandemic years (2015-2019) and then assume that each week in 2020-2022 be like its pre-Covid average (the “baseline”.)

Excess death is then calculated as the difference between that baseline and the deaths that actually occurred. Reasonable enough.

But OWID use a slightly more complex model to estimate “baseline” deaths.

I contacted OWID, and they directed me to their projection data source — the World Mortality Dataset (“WMD”...) which says their baseline is calculated using “linear extrapolation” of 2015-2019.

That is a simple projection model, and is often reasonable to use. It means they look at the trendline over 2015-2019, and then assume the trend would have continued over 2020-2022, had there had been no pandemic.¹

Let’s see what that trendline looked like:

The graph shows that Sweden had a slightly falling trendline pre-Covid, and the reason lies mostly in the last year, 2019, in which Sweden experienced a particularly mild flu season.

The brown line below shows what OWID/WMD projected baseline deaths to be, in the absence of Covid:

Note: I truncated the y-axis for better visibility of dataset differences. That also causes the red line to appear steeper, but it’s actually the same

In contrast, the OECD (black line) above considers only the pre-Covid average.

As time goes on, the OWID estimate becomes increasingly influenced by the trendline, and if you squint, you can see that the two datasets’ estimates are further apart in 2022 than in 2020.

The difference sure looks trivial, but cumulatively, it adds up to a real difference in excess mortality.

Next, let’s plot actual deaths on top of the projections:

We can clearly see the death spikes caused by original Covid and Delta. But when Omicron hit in winter 2021, deaths were only a little worse than pre-Covid winters.

Cumulatively, the different methods add up

The above graph (subtracting the brown and black lines from the blue) is how I calculated this cumulative excess deaths graph we saw at the very start:

OWID’s single methodological difference of using the trendline for prediction makes Sweden’s cumulative excess mortality 25% higher (yellow line) than the fixed OECD data (light-blue line.)

So now we know why the two measures are different. But which methodology is the better one?

Which method is right? Should the trendline method be used?

Linear extrapolation, as used by WHO/OWID/WMD, particularly makes sense when a country is rapidly improving its technology or health habits. If you have a rapidly-improving country, it would be foolish to predict future years without considering a strong trend.

On the other hand, if a trend slopes downward because of a fluke — such as merely happening to avoid a particular flu strain one year — then using the trend would actually be mis-informative about future years. It would be more correct to take the average instead.

So to determine which approach is better, we need to answer this question: Was Sweden’s downward trend due to generally improving conditions, or to one lucky year at the end?

To answer that, I first checked the importance of 2019.

2019 stands out, having 3,375 fewer deaths than 2018.

What would happen if 2019 were removed from the trendline estimate? Using OWID’s code, I removed 2019, and that totally removed the downward trend.

But we can’t just remove 2019 because it was low. We need to know why it was low: because of a fluke, or a general trend?

It’s often noted that Sweden had a mild flu season that fall. But looking at Swedish data, there were 710 fewer respiratory deaths in Sweden in 2019, compared to 2018. So that explains 1/5th of the fall in deaths.

It turns out that the big decline was in heart-related deaths. 2,000 fewer people died of that in 2019, vs 2018. Also, it was falling consistently over a long period of time, since the 1990s (blue line below.)

Graph built using data from socialstyrelsen.se

Now, heart-related deaths fell extra fast in 2019. That extra speed may have been due to a lower flu virus load. I didn’t know this, but it turns out that having the flu increases heart disease risk significantly.

Swedish health authorities also believed low flu load to be a major factor in 2019’s low deaths.

If long-term trends from 1997-2018 had continued, I calculate that there would’ve been 1,000 fewer heart-related deaths in 2019, rather than the 2,000 fewer that were actually experienced.² So let's say that the remaining 1,000 were caused by the "fluke" reduced viral load that the country experienced that year.

Going by that logic, about half of the reduced deaths (1,500 out of 3,375) were due to a low flu/cold season, while the rest were the result of long-run positive health trends in Sweden.

Factoring in “dry tinder”

The above could justify taking the average of OWID and the fixed OECD estimate. However, it also needs to be considered that a mild virus season not only depresses deaths in the year it occurs, but it also leaves more vulnerable people alive for the grim reaper to take in the following year.

This was referred to in the academic literature as “dry tinder”, and studies agree that it was a factor in the 2020 death toll (also, it was not nearly the dominant factor. Covid was.)

For example, this preprint paper estimates that there were about 6,000 extra vulnerable Swedes at the start of 2020 than is typical.

The “dry tinder” effect is a particular danger for trendline analysis. The trendline is supposed to pick up consistent trends, but if a trend points downward because of one good year that leaves lots of “dry tinder” for the following year, the trendline will predict a fall for the next year even when the opposite is likely to happen.

Given all that, I think the best estimate is to just use the OECD’s methodology (but also to fix OECD’s data to include deaths with an unknown week.)

Comparing Sweden with its neighbors, using the best methods and data

Here’s what happens when we use OECD’s simple methodology, while using OWID’s dataset that correct assigns deaths with unknown weeks:

Norway and Sweden are now essentially tied, while Sweden did better than Denmark.

This chart still suggests that Norway did better than Sweden as long as it was keeping Covid out using strict travel bans. After it lifted those, however, it turned out that the deaths it prevented were merely deferred for about a year.

Overall, I feel comfortable about this as a best estimate, based on all the above reasoning. There is certainly room for quibbling about exactly how much to consider things like heart disease deaths, and dry tinder, but things like that are unlikely to change the big picture.

Conclusion

— Sweden did in fact do the best of any country in Europe (or, at least, tied with Norway) when all factors are considered and the most appropriate data and methods are used.

— Sweden’s success without lockdowns suggests that western lockdowns were really not effective beyond the very short run. We can now be even more sure of that than we were previously.

— It’s worth further investigation about exactly why Sweden did well compared to its neighbors despite no lockdowns. Could early theories, such as letting young “superspreaders” get natural immunity to slow spread later, have had validity?

— It can take a lot of work to get to the bottom of conflicting datasets!

1. OWID/WMD do something just slightly more complicated than applying the red trendline in my graph; they do a regression with “time fixed effects” which seems reasonable. That gives them somewhat higher baseline deaths than they’d get if they just applied the red trendline.

2. Or, taking a different time period: if trends from 2015-2018 had continued, I calculate that there would’ve been 500 fewer heart-related deaths in 2019, not 2,000 fewer.